3次元圧縮性流体解析の基礎方程式
(1)質量保存式
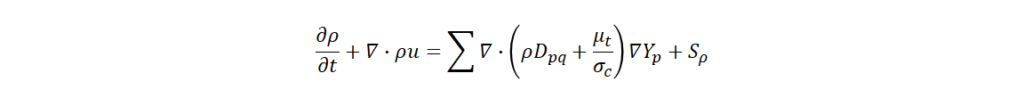
(2)運動量保存式
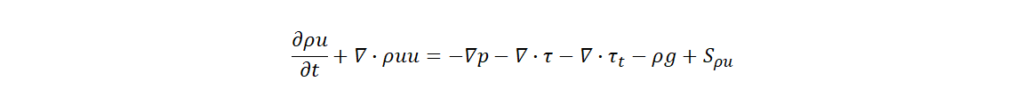
(3)エネルギー保存式
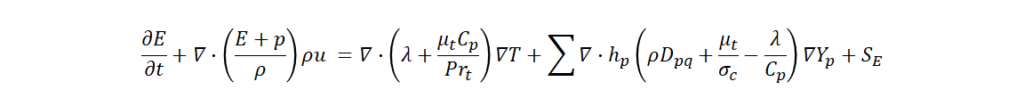
(4)成分ガス濃度の質量保存式
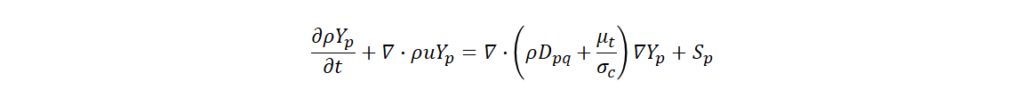
ρ :流体密度、t :時間、u:流速、Dpq :成分 p と q の相互拡散係数、μt:乱流粘性係数、σc :乱流 Schmidt 数、Yp : p 成分の質量分率、Sρ , Sρu , SE , Sp :各保存式の生成消滅項を示す。p :流体圧力(以下、単に圧力) 、τ :剪断応力、 τt :乱流運動量束、g:重力加速度、E :全エネルギー、Cp :定圧比熱、Prt :乱流 Prandtl 数、T :流体温度(以下、単に温度)、hp :ガス成分のエンタルピー、λ:熱伝導度を示す。
高速化・安定化のために採用した方法
(1)新たな陰解法として、圧力、流速、エネルギーが強く結びついた ECBA 法を開発
(2)圧力と流速の連成方法として SIMPLEC 法に基づく方法の採用
① SIMPLE 法 ⇒ 収束性が悪い、圧力が破綻しやすい
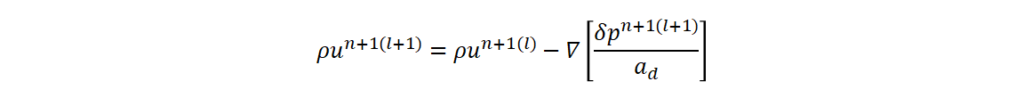
② SIMPLE 法 ⇒ SIMPLE 法を改善
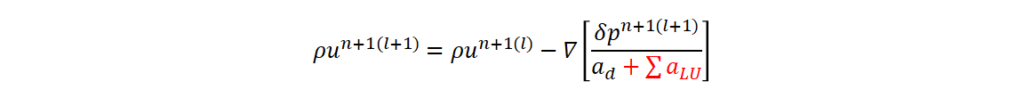
(3)成分ガス濃度の質量保存式、密度の質量保存式およびエネルギー保存式における生成消滅項線形化の工夫
凝縮や反応による物質の生成消滅項 ![]() を Taylor 展開による線形化と、かつ、物質の質量分率がゼロ以下、1.0 以上にならないようにすることにより比較的大きな時間スケールで安定的な計算が可能、次式右辺第 1 項を成分ガス濃度の質量保存式、密度の質量保存式およびエネルギー保存式の左辺、次式第 2 項と第 3 項を成分ガス濃度の質量保存式、密度の質量保存式およびエネルギー保存式の右辺に配置
を Taylor 展開による線形化と、かつ、物質の質量分率がゼロ以下、1.0 以上にならないようにすることにより比較的大きな時間スケールで安定的な計算が可能、次式右辺第 1 項を成分ガス濃度の質量保存式、密度の質量保存式およびエネルギー保存式の左辺、次式第 2 項と第 3 項を成分ガス濃度の質量保存式、密度の質量保存式およびエネルギー保存式の右辺に配置
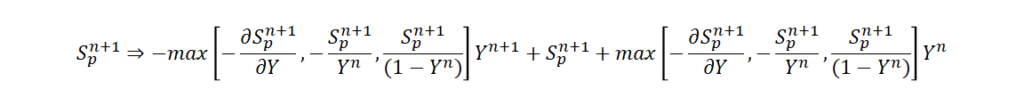
(4)最新の行列反復解法ライブラリ Lis の採用
ECBA 法
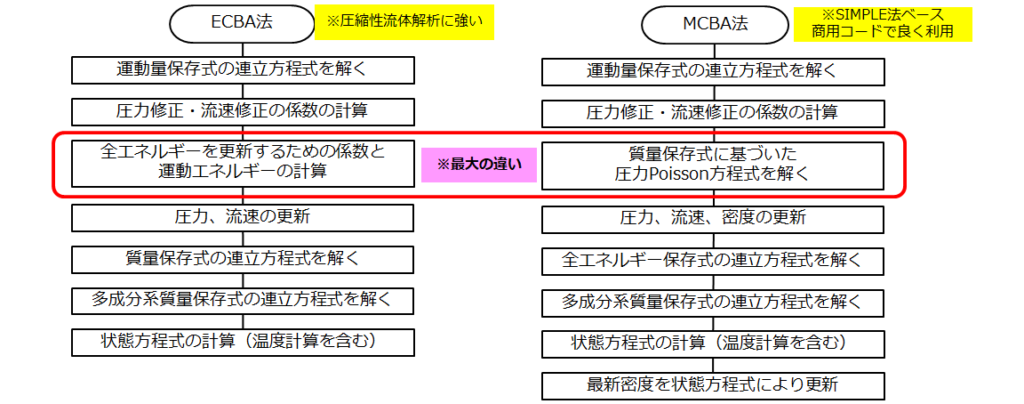
(1)ECBA : Energy Conservation Based Algorithm
(2)数値計算法の根幹である圧力 Poisson 方程式を、これまでの SIMPLE 法系列の質量保存式ではなく、エネルギー保存式に基づいて組み立て、圧力、流速、エネルギーが強く結びついた解法を独自に開発した。
(3)変形したエネルギー保存式(赤く示した項を両辺に追加)
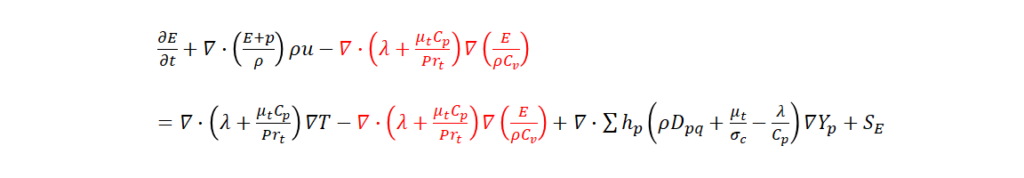
の左辺の全エネルギー E と運動量束 ρu を次式に置き換えて離散化することで得られる圧力修正量 ![]() に関する圧力 Poisson 方程式の連立方程式を解く。
に関する圧力 Poisson 方程式の連立方程式を解く。
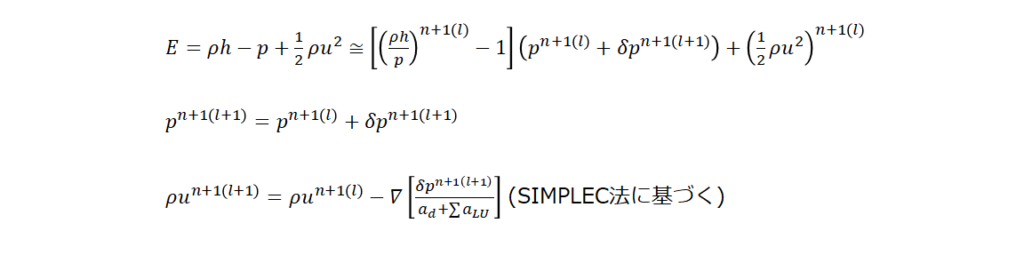
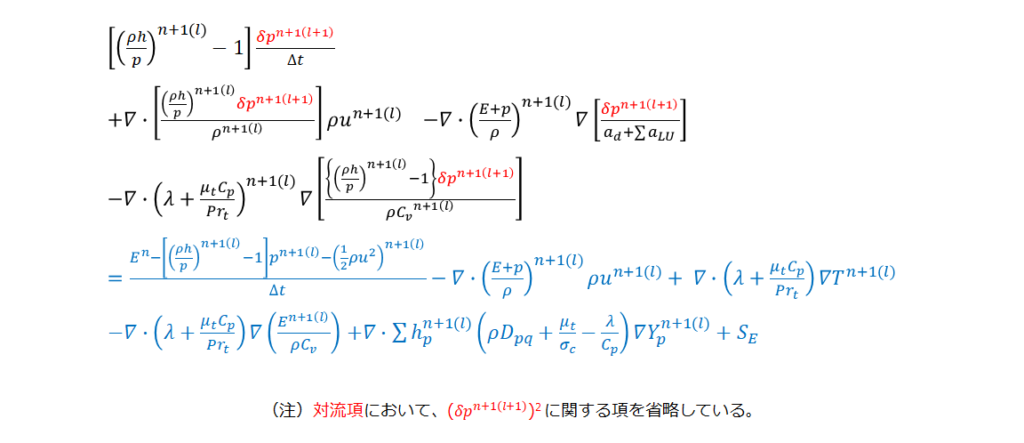
圧力 Poisson 方程式は次のように簡単に示すと、未知数である ![]() に関する連立方程式としてまとめられる。右辺は荷重項として代数的に求める。
に関する連立方程式としてまとめられる。右辺は荷重項として代数的に求める。
ECBA 法は MCBA 法 (SIMPLEC 法)と比べて、次のような特徴を持っている。
| No. | 項目 | ECBA 法 | MCBA 法 (SIMPLEC 法) |
| 1 | 質量の保存性 | 質量とエネルギーの保存式を適切に解くため、保証される。 | 圧縮性考慮のために保存式から得られた密度を状態方程式で得られる密度に置き換えるため、保証されない。 |
| 2 | 密度差が大きい流れ | 圧縮性を効果的に取り入れているため、密度差の大きい流れでも適切に計算できる。 | 圧縮性が効果的に入らないため、密度の大きい流体が密度の小さい流体に衝突した場合、密度の小さい流体が加速されすぎて不自然な流れになることがある。 |
| 3 | 熱的に大きな上昇を伴う流れ | 圧力、流速、エネルギーが強く結びついた解法のため、特別な処理なく適切に計算できる。 | 突発的に大きな熱発生があった場合、エネルギー変化に対して圧力や流速の変化が追い付けず、温度が異常になることがある。この場合、エンタルピーを状態方程式で得られるエンタルピーに置き換えることで改善することがある。 |
| 4 | 大きい乱流変動に誘起されるエネルギー・圧力変動 | 圧力、流速、エネルギーが強く結びついているため、流速変動→乱流変動→乱流拡散によるエネルギー変動→圧力変動→流速変動といった負のサイクルが生じて異常な熱流動変化になることがある。 | 圧力、流速とエネルギーの結びつきが弱く、左記の負のサイクルが生じにくい。 |
水蒸気凝縮モデル/壁構造物熱伝達モデル
(1)バルク凝縮モデル
飽和水蒸気圧を超えた量を凝縮緩和時間で凝縮させるモデル
凝縮時は潜熱を考慮するものの、凝縮した水蒸気の質量、エネルギーは計算体系から削除
(2)壁面凝縮モデル
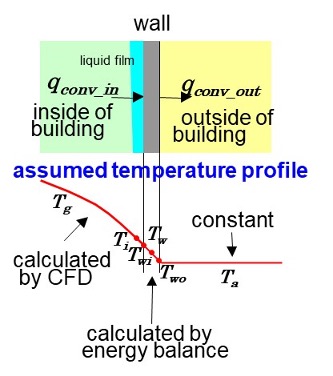
液膜を仮定し気体と液膜との熱伝達、液膜と壁面との熱伝達および凝縮に伴う熱伝達の熱収支に基づくモデル
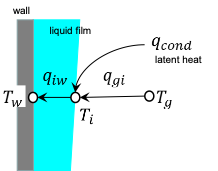
(3)壁構造物熱伝達モデル
厚みを考慮した壁の内外の熱伝達と壁の熱伝導による熱収支に基づくモデル
FP エアロゾル挙動解析モデル
(1)基礎方程式
エアロゾル濃度をパッシブスカラー(トレーサー)とした対流拡散方程式
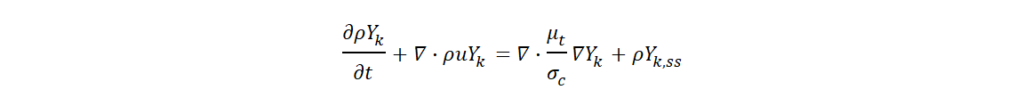
(2)拡散・慣性衝突による乱流沈着速度 [1]

(3)重力沈降速度
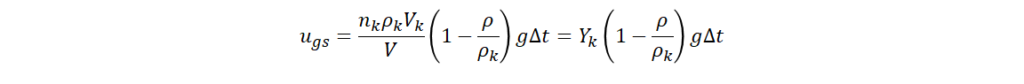
(4)凝集による生成消滅
乱流運動衝突、浮力・重力衝突、層流剪断衝突による凝集 [2]
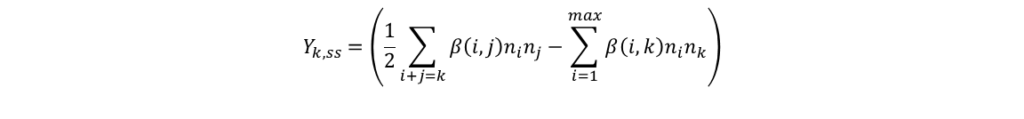

ρ:流体密度、Yk :エアロゾル濃度(添字の k は粒径クラス)、t :時間、u :流速、μt :乱流粘性係数、σc :乱流 Schmidt 数、Yk,ss :エアロゾル濃度の生成消滅、vk:エアロゾルの沈着速度、vdk :拡散による沈着速度、U+:摩擦速度、vlk :慣性衝突による沈着速度、Re:Reynolds 数、ugs :重力沈降速度、nk : k 番目の粒子グループの粒子数、ρk :エアロゾル密度、Vk :粒子 1 個の体積、 V :格子体積、 g :重力加速度、β(i , j):粒子グループ i , j の衝突速度、ni :粒子径グループ i の数密度を示す。
