亀裂進展プログラムの開発
背景
社会インフラやプラント等の設備の長寿命化にともない、その材料の劣化の診断や予測が、社会として取り組むべき大きな課題となっています。その安全性を確立する要素技術のひとつとして、亀裂進展に関する研究テーマがあります。このテーマの研究内容については、実験や理論がほとんどであるが、計算機シミュレーションでもいくつかの研究の取り組みが開始されているのが現状です。
現在、提案されている手法は、大きく分けて、ミクロなモデルとマクロなモデルがあります。前者については、第一原理計算を利用した原子レベルからの亀裂進展の機構解明に関するモデルであり、当社が参加している文部科学省の戦略的基盤ソフトウェアの開発プロジェクトや革新的戦略ソフトウェアの開発プロジェクトでも実施され、いくつかの成果を上げています。一方、後者については、実験や理論から得られたモデルを利用したシミュレーション、および、FEM等のマクロな手法に亀裂のモデル化を組み込んだシミュレーションが実施されています。ここでは、マクロモデルを利用した亀裂進展の実績について述べます。
概要
従来実施されてきたマクロな手法を利用した亀裂の解析では、亀裂の位置を固定して、その周辺の情報を得ることを目的とし、ある程度の成果を上げています。さらに、この手法を発展させた亀裂進展の解析では、格子に依存しない亀裂の進展をさせることが重要です。その目的で、EFGMやXFEM等の手法を亀裂進展の解析が着目されています [1][2][3][4] 。ここでは、Belytschkoらの方法にしたがって求めた計算例を示します。計算手法は、亀裂の先端をモデル化するために、通常の離散化をenrichした形で、つぎのような定式化をしています。
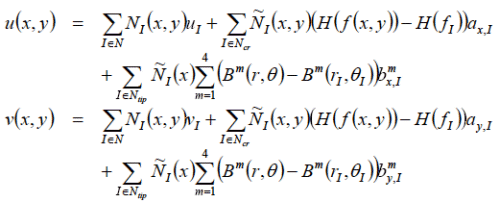
ここで、節点での変数が
であり、節点の種類に依存してこのうちからいくつかの変数が選択されます。具体的には、前者2つが通常の自由度であり、3,4番目はcrackの場合に追加される自由度、5番目以降はtipsの場合に追加される自由度です。 
は形状関数、
はcrack curveから
までの符号付距離、 
は1か－1の値をとるヘビサイド関数であり、 
はつぎの通りです。
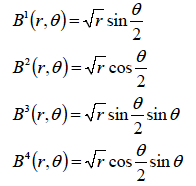
ここで、
はtipsの座標
を中心として、crackの先端の方向を0radとする局所の局座標です。また、亀裂進展の方向は応力拡大係数により評価します。その方向に微小な量だけ亀裂を進展させ、それを時間発展的に解きます。この定式化による計算例を示します。
（手塚明(産業技術総合研究所)・松原聖(アドバンスソフト)による,2005）
この方法による亀裂の進展は、メッシュの位置に依存しないため、あらかじめ亀裂を意識したメッシュを設定する必要がないことが最大の利点であり、応用範囲は広いと考えられます。亀裂進展のマクロモデルの今後の課題として、これらのモデルの検証および計算コストを抑えた３次元化の手法の開発が挙げられます。当社でも、これらの手法に着目し、産業界での実用化を目的としたソフトウェア開発およびその適用に取り組んでいく計画です。
参考文献
[1] Ventura G, Budyn E, Belytschko T,”Vector level sets for description of propagating cracks in finite elements,” INT J NUMER METH ENG 58 (10): 1571-1592 NOV14 2003
[2] Dolbow J, Moes N, Belytschko T,”Discontinuous enrichment in finite elements with a partitionof unity method,” FINITE ELEM ANAL DES 36 (3-4): 235-260 NOV 1 2000
[3] Moes N, Dolbow J, Belytschko T A finite element method,”for crack growth without remeshing ,” INT J NUMER METH ENG 46(1): 131-150 SEP 10 1999
[4] Belytschko T, Chen H, Xu JX, et al.,,”Dynamic crack propagation based on loss of hyperbolicity and a new discontinuous enrichment,” INT J NUMER METH ENG 58 (12):1873-1905 NOV 28 2003